Наша стагоддзе - стагоддзе хуткасці і вялізнага патоку інфармацыі. Хуткасць камунікацый і аб'ём інфармацыі расце па экспаненце. З усяго інфармацыйнага патоку велізарны працэнт складае інфармацыйнае смецце, і толькі нязначная колькасць інфармацыі карысная і вартая ўвагі.
Медыяпісьменнасць - неабходны навык ў век лічбавых тэхналогій. Гэта ўменне добра арыентавацца ў розных тыпах медыя і разумець іх сутнасць. Мы цяпер атрымліваем вялікую колькасць інфармацыі з розных крыніц. Але ўсе медыярэсурсы аб'ядноўвае адно: хтосьці іх стварыў і па нейкай прычыне. Менавіта разуменне гэтай прычыны і ляжыць у аснове медыяпісьменнасці.
Медыяпісьменнасць дапамагае вызначаць, ці сапраўды тое ці іншае інфармацыйнае паведамленне заслугоўвае даверу. Яна таксама дазваляе распазнаваць спецыяльныя метады, якія выкарыстоўваюць маркетолагі ў рэкламе, каб пераканаць людзей купіць тавар.
Цяпер ствараць медыя можа кожны. Таму стала цяжэй даведацца, хто аўтар паведамлення і ці можна яму давяраць. Менавіта крытычнае мысленне дасць магчымасць не патрапіць у пастку. Наша задача - навучыць дзяцей самастойна ацэньваць розныя сродкі камунікацыі, вызначаць, наколькі адэкватны ў іх кантэнт, чаму была ўключана тая ці іншая інфармацыя, наколькі поўна раскрыта тэма, якія асноўныя ідэі медыяпаведамлення.
А яшчэ важна навучыць дзяцей распазнаваць пункт гледжання аўтара і фармаваць ўласнае меркаванне па розных пытаннях на аснове інфармацыі, якую яны ўжо ведаюць.
Не менш важна разумець мэты аўтара. Ці з'яўляецца паведамленне чыста інфарматыўным, ці аўтар спрабуе памяняць наша меркаванне, а можа, распавядае нам пра новыя ідэі, пра якія мы ніколі не чулі? Калі дзеці разумеюць, які ўплыў на іх можа аказаць медыя, разумеючы яго сапраўдную мэту, яны могуць зрабіць усвядомлены выбар.
Таксама важна навучыцца адказна ствараць медыяпаведамленні. Гарантыя эфектыўнай камунікацыі - прызнаваць уласны пункт гледжання, ацэньваць, што і як мы кажам, разумець, што кожнае наша паведамленне аказвае ўплыў на іншых.
Адзіны спосаб развіць уменне арыентавацца ў інфармацыйнай прасторы, засцерагчы сябе ад уздзеяння маніпуляцый - выпрацаваць звычку задаваць сабе канкрэтныя пытанні, навучыцца крытычна думаць і выпрацаваць моцны «імунітэт» супраць інфармацыйнага смецця.
Большая частка нашых кагнітыўных працэсаў адбываецца аўтаматычна, і ў цэлым гэта карысна і зручна. Праблема здараецца, калі мы давяраем гэтым аўтаматызмам кіраваць важнымі для нас рашэннямі. Без здольнасці крытычна думаць мы становімся лёгкай мішэнню для маніпуляцый, і гэта можа прывесці да катастрафічных вынікаў.
Крытычнае мысленне ўяўляе сабой мэтанакіраваную і структураваную апрацоўку інфармацыі, якая дапамагае прымаць больш эфектыўныя рашэнні і ў цэлым лепш разумець свет.
Мне як настаўніку матэматыкі важна навучыць дзяцей крытычна думаць і не трапляць на інфармацыйныя "кручкі" сусветнага павуціння. Займаючыся на курсе, я стала больш задумвацца над тым, каб на ўроках не слепа прытрымлівацца падручніка, а працаваць з дзецьмі так, каб яны атрымлівалі веды і ўменні для жыцця ў соцыуме.
Не сакрэт, што крытычнае мысленне развіваецца ў ходзе пошуку адказу на самыя розныя пытанні. Задаючы вучням пытанні, мы стымулюем іх актыўнасць, ўважлівасць.
У сваёй практыцы рэгулярна арганізую на занятках працу ў мікрагрупах, каб развіць навыкі ўзаемадзеяння і сумеснага пошуку вырашэння праблем і прапаную вучням задачы адкрытага тыпу.
 Мал. 1 Мал. 1 |
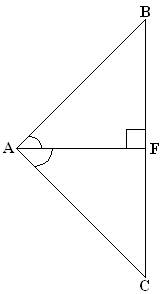
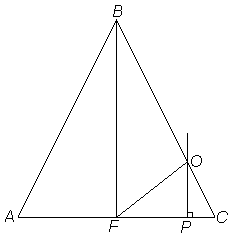
1. Напрыклад, на ўроку абагульнення і сістэматызацыі ведаў па тэме «Паралельныя прамыя» сямікласьнікам можна прапанаваць наступную задачу адкрытага тыпу: «Адрэзак BF - медыяна роўнабаковага трохвугольніка ABC (AB = BC). Пункт O ляжыць на старане BC, адрэзак OP - вышыня трохвугольніка FOC (мал. 1) ». У выніку работы вучні сфармулююць пытанне: «Ці з'яўляюцца прамыя BF і OP паралельнымі?» |
|
Мал. 2 |
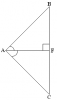
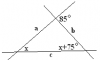
2. У трохвугольніку ABC AF - бісектрыса вугла BAC, вугал BFA = вуглу CFA = 90º, вугал ABF = 70º (мал. 2).
Прааналізаваўшы ўмова задачы і, давёўшы, што трохвугольнік ABC - роўнабаковы, вучні могуць сфармуляваць пытанне задачы: «Вылічыць градусныя меры вуглоў трохвугольніка ABC».
|
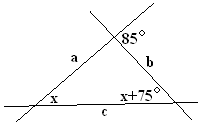
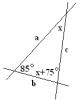
3. Прамыя a і b перасякаюцца пад вуглом 85º. Прамая c перасякае a і b так, што рознасць ўнутраных аднабаковых вуглоў роўна 75º. Вылічыце градусныя меры гэтых вуглоў. Магчыма, тут варыянты з'яўляюцца некалькі нечакана для вучняў, бо для пабудовы прамой с магчымыя дзве сітуацыі (мал. 3 і мал. 4):
 Мал. 3 Мал. 3 |
Мал. 4 |
|
У гэтым выпадку маем: 85°+х°+х°+75°=180° Тут атрымліваем: х=10°, 85°. Адказ: 10° и 85° или 5° и 80°. |
Магчыма і такое размяшчэнне прамых. 180°–85°+х°+х°+75°=180° х=5°, 80°. |
Яшчэ ў сваёй практыцы часта выкарыстоўваю такі прыём як «складанне задачы». Дзецям прадастаўляецца чарцёж, па якім трэба скласці сваю задачу (пісьменна і прыгожа), затым я агучваю тую, якая была першапачаткова задумана мною. Варта адзначыць, што навучэнцам вельмі падабаецца быць у ролі складальнікаў задач.
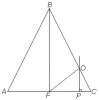
4. У трохвугольніку АВС праведзены адрэзак DК так, што вугал КDС роўны вуглу АВС, AD = 4 см, DС = 6 см, КС = 5 см. Знайдзіце даўжыню адрэзка ВК.
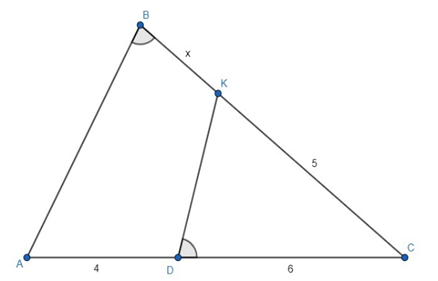
Мал. 5
Вучні павінны памятаць, што часта самыя эфектыўныя рашэнні дзівяць не складанасцю, а прастатой. Таму варта імкнуцца знайсці простае рашэнне.
Параўнанне (супастаўленне) - ключавы метад навучання дзяцей крытычнаму мысленню.
На ўроках дзеці ўжо прывыклі, што ў працэсе работы над задачай мы разглядаем некалькі варыянтаў яе рашэння.
Напрыклад, знайдзіце нулі функцыі: y = (x –1)2 - 4.
Часцей за ўсё навучэнцы не задумваюцца над спосабамі рашэння. Прыраўноўваюць да нуля, шаблонна раскрываюць дужкі, прыводзяць падобныя складнікі і знаходзяць карані квадратнага ўраўнення.
А можна заўважыць, што злева запісаная рознасць квадратаў ((x –1)2 – 4 = 0), і задача зводзіцца да вырашэння лінейных ураўненняў. А калі лік -4 перанесці направа? (x –1)2 = 4.
Мазгавы штурм - дзейсны метад развіцця крытычнага мыслення. Прыкладам сітуацыі развіцця крытычнага мыслення з дапамогай гэтага спосабу можа стаць арганізацыя групавога абмеркавання праблемнага пытання.
Пры якім значэнні параметра р ўраўненне мае адзіны корань:
(1-p) x2 + 4px – 1 = 0 ?
Вучні аналізуюць ураўненне і робяць выснову: яно мае адзіны корань ў двух выпадках:
а) ураўненне квадратнае і D = 0;
б) урараўненне лінейнае і мае адзінае рашэнне
У выпадку а) вылічым D/4 = (2p)2 – (1 – p) (-1) = 4p2 – p +1. Прыраўнаўшы дыскрымінант да нуля, атрымліваем ураўненне, якое не мае рашэнняў.
Разгледзім выпадак б) 1 – p = 0, p = 1.
Адказ: 1.
На гэтым прыкладзе я вучу дзяцей быць уважлівымі да тэксту, да слова. Часта вучні не звяртаюць увагі на тое, што ў ўмове не пазначана, што дадзенае ўраўненне з'яўляецца квадратным, і не задумваюцца, што ўраўненне можа быць лінейным.
Яшчэ добры спосаб развіцця навыкаў медыяпісьменнасці і ўмення крытычна думаць - рашэнне практыка-арыентаваных задач.
Мы з дзецьмі паспрабавалі стаць паспяховымі рэкламнымі агентамі, паверыўшы аб'яве.
Гарантаваны месячны заробак рэкламнага агента - 300 рублёў. Кожны знойдзены агентам кліент прыносіць яму дадатковы даход, які складае 5% ад сумы дагавора. Фірма, у якой працуе агент, заключае дамовы толькі ад сумы не менш за 250 руб. Высветліце, на якую суму ў месяц неабходна заключыць дагавор агенту, каб яго заробак складаў не менш за 850 руб. Колькі кліентаў, якія заключылі дагавор на 250 руб., трэба прыцягнуць агенту, каб зарабіць у месяц 850 рублёў?
Якое ж было здзіўленне дзяцей, што неабходная сума роўная 10 000 рублям, а кліентаў павінна быць мінімум 44. Дзеці правялі цікавую рэфлексію і зрабілі важныя для сябе высновы. «Вось і вер цяпер абяцанням працадаўцоў», - рэзюмаваў адзін з вучняў.
Дзелячыся фрагментам свайго вопыту, я хачу падкрэсліць велізарны патэнцыял урокаў матэматыкі ў развіцці крытычнага мыслення. Упэўненая, кожны з нас можа на сваіх уроках навучыць дзяцей дэкадаваць (аналізаваць) медыяматэрыялы; распазнаваць хлусню і маніпуляцыйныя прыёмы, знаходзіць фэйкі, заўважаць прыхаваную рэкламу, а таксама крытычна і рэфлексіўна ставіцца да любой інфармацыі.
Мне запомнілася, як адзін з падлеткаў сваімі словамі растлумачыў, што такое крытычнае мысленне: гэта здольнасць асобы мець уласнае меркаванне адносна ўсяго, што адбываецца навокал. Менавіта гэтаму і вучыць курс Медыяпісьменнасць.
Вялікі дзякуй арганізатарам і калегам за супрацоўніцтва і цікавую вучобу. Было выдатна!
Людміла Шляжко,
настаўніца матэматыкі, студэнтка дыстанцыйнага курса "Медыяадукацыя ў школе" - 2021.
настаўніца матэматыкі, студэнтка дыстанцыйнага курса "Медыяадукацыя ў школе" - 2021.
Спампаваць матэрыял на рускай мове